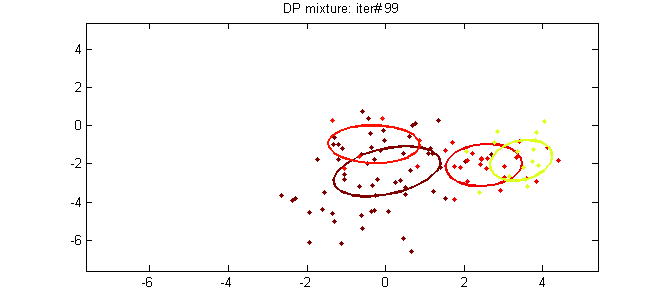
 This article is the fifth part of the tutorial on Clustering with DPMM. In the previous posts we covered in detail the theoretical background of the method and we described its mathematical representationsmu and ways to construct it. In this post we will try to link the theory with the practice by introducing two models DPMM: the Dirichlet Multivariate Normal Mixture Model which can be used to cluster Gaussian data and the Dirichlet-Multinomial Mixture Model which is used to cluster documents.
This article is the fifth part of the tutorial on Clustering with DPMM. In the previous posts we covered in detail the theoretical background of the method and we described its mathematical representationsmu and ways to construct it. In this post we will try to link the theory with the practice by introducing two models DPMM: the Dirichlet Multivariate Normal Mixture Model which can be used to cluster Gaussian data and the Dirichlet-Multinomial Mixture Model which is used to cluster documents.
Update: The Datumbox Machine Learning Framework is now open-source and free to download. Check out the package com.datumbox.framework.machinelearning.clustering to see the implementation of Dirichlet Process Mixture Models in Java.
The first Dirichlet Process mixture model that we will examine is the Dirichlet Multivariate Normal Mixture Model which can be used to perform clustering on continuous datasets. The mixture model is defined as follows:
![]()
![]()
![]()
Equation 1: Dirichlet Multivariate Normal Mixture Model
As we can see above, the particular model assumes that the Generative Distribution is the Multinomial Gaussian Distribution and uses the Chinese Restaurant process as prior for the cluster assignments. Moreover for the Base distribution G0 it uses the Normal-Inverse-Wishart prior which is conjugate prior of Multivariate Normal distribution with unknown mean and covariance matrix. Below we present the Graphical Model of the mixture model:
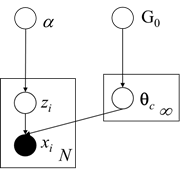
Figure 1: Graphical Model of Dirichlet Multivariate Normal Mixture Model
As we discussed earlier, in order to be able to estimate the cluster assignments, we will use the Collapsed Gibbs sampling which requires selecting the appropriate conjugate priors. Moreover we will need to update the parameters posterior given the prior and the evidence. Below we see the MAP estimates of the parameters for one of the clusters:
![]()
![]()
![]()
![]()
![]()
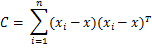
Equation 2: MAP estimates on Cluster Parameters
Where d is the dimensionality of our data and ![]() is the sample mean. Moreover we have several hyperparameters of the Normal-Inverse-Wishart such as the μ0 which is the initial mean, κ0 is the mean fraction which works as a smoothing parameter, ν0 is the degrees of freedom which is set to the number of dimensions and Ψ0 is the pairwise deviation product which is set to the dxd identity matrix multiplied by a constant. From now on all the previous hyperparameters of G0 will be denoted by λ to simplify the notation. Finally by having all the above, we can estimate the probabilities that are required by the Collapsed Gibbs Sampler. The probability of observation i to belong to cluster k given the cluster assignments, the dataset and all the hyperparameters α and λ of DP and G0 is given below:
is the sample mean. Moreover we have several hyperparameters of the Normal-Inverse-Wishart such as the μ0 which is the initial mean, κ0 is the mean fraction which works as a smoothing parameter, ν0 is the degrees of freedom which is set to the number of dimensions and Ψ0 is the pairwise deviation product which is set to the dxd identity matrix multiplied by a constant. From now on all the previous hyperparameters of G0 will be denoted by λ to simplify the notation. Finally by having all the above, we can estimate the probabilities that are required by the Collapsed Gibbs Sampler. The probability of observation i to belong to cluster k given the cluster assignments, the dataset and all the hyperparameters α and λ of DP and G0 is given below:
![]()
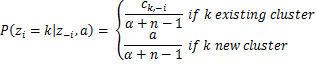
![]()
Equation 3: Probabilities used by Gibbs Sampler for MNMM
Where zi is the cluster assignment of observation xi, x1:n is the complete dataset, z-i is the set of cluster assignments without the one of the ith observation, x-i is the complete dataset excluding the ith observation, ck,-i is the total number of observations assigned to cluster k excluding the ith observation while ![]() and
and ![]() are the mean and covariance matrix of cluster k exluding the ith observation.
are the mean and covariance matrix of cluster k exluding the ith observation.
The Dirichlet-Multinomial Mixture Model is used to perform cluster analysis of documents. The particular model has a slightly more complicated hierarchy since it models the topics/categories of the documents, the word probabilities within each topic, the cluster assignments and the generative distribution of the documents. Its target is to perform unsupervised learning and cluster a list of documents by assigning them to groups. The mixture model is defined as follows:
![]()
![]()
![]()
![]()
Equation 4: Dirichlet-Multinomial Mixture Model
Where φ models the topic probabilities, zi is a topic selector, θk are the word probabilities in each cluster and xi,j represents the document words. We should note that this technique uses the bag-of-words framework which represents the documents as an unordered collection of words, disregarding grammar and word order. This simplified representation is commonly used in natural language processing and information retrieval. Below we present the Graphical Model of the mixture model:
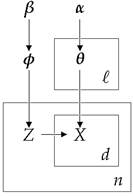
Figure 2: Graphical Model of the Dirichlet-Multinomial Mixture Model
The particular model uses Multinomial Discrete distribution for the generative distribution and Dirichlet distributions for the priors. The ℓ is the size of our active clusters, the n the total number of documents, the β controls the a priori expected number of clusters while the α controls the number of words assigned to each cluster. To estimate the probabilities that are required by the Collapsed Gibbs Sampler we use the following equation:
![]()
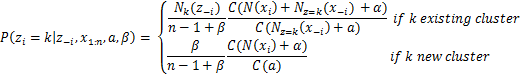
Equation 5: Probabilities used by Gibbs Sampler for DMMM
Where Γ is the gamma function, zi is the cluster assignment of document xi, x1:n is the complete dataset, z-i is the set of cluster assignments without the one of the ith document, x-i is the complete dataset excluding the ith document, Nk(z-i) is the number of observations assigned to cluster k excluding ith document, Nz=k(x-i) is a vector with the sums of counts for each word for all the documents assigned to cluster k excluding ith document and N(xi) is the sparse vector with the counts of each word in document xi. Finally as we can see above, by using the Collapsed Gibbs Sampler with the Chinese Restaurant Process the θjk variable which stores the probability of word j in topic k can be integrated out.
2013-2024 © Datumbox. All Rights Reserved. Privacy Policy | Terms of Use
Leave a Reply