 In the previous articles we discussed in detail the Dirichlet Process Mixture Models and how they can be used in cluster analysis. In this article we will present a Java implementation of two different DPMM models: the Dirichlet Multivariate Normal Mixture Model which can be used to cluster Gaussian data and the Dirichlet-Multinomial Mixture Model which is used to clustering documents. The Java code is open-sourced under GPL v3 license and can be downloaded freely from Github.
In the previous articles we discussed in detail the Dirichlet Process Mixture Models and how they can be used in cluster analysis. In this article we will present a Java implementation of two different DPMM models: the Dirichlet Multivariate Normal Mixture Model which can be used to cluster Gaussian data and the Dirichlet-Multinomial Mixture Model which is used to clustering documents. The Java code is open-sourced under GPL v3 license and can be downloaded freely from Github.
Update: The Datumbox Machine Learning Framework is now open-source and free to download. Check out the package com.datumbox.framework.machinelearning.clustering to see the implementation of Dirichlet Process Mixture Models in Java.
The code implements the Dirichlet Process Mixture Model with Gibbs Sampler and uses the Apache Commons Math 3.3 as a matrix library. It is licensed under GPLv3 so feel free to use it, modify it and redistribute it freely and you can download the Java implementation from Github. Note that you can find all the theoretical parts of the clustering method in the previous 5 articles and detailed Javadoc comments for implementation in the source code.
Below we list a high level description on the code:
The DPMM is an abstract class and acts like a base for the various different models, implements the Chinese Restaurant Process and contains the Collapsed Gibbs Sampler. It has the public method cluster() which receives the dataset as a List of Points and is responsible for performing the cluster analysis. Other useful methods of the class are the getPointAssignments() which is used to retrieve the cluster assignments after clustering is completed and the getClusterList() which is used to get the list of identified clusters. The DPMM contains the static nested abstract class Cluster; it contains several abstract methods concerning the management of the points and the estimation of the posterior pdf that are used for the estimation of the cluster assignments.
The GaussianDPMM is the implementation of Dirichlet Multivariate Normal Mixture Model and extends the DPMM class. It contains all the methods that are required to estimate the probabilities under the Gaussian assumption. Moreover it contains the static nested class Cluster which implements all the abstract methods of the DPMM.Cluster class.
The MultinomialDPMM implements the Dirichlet-Multinomial Mixture Model and extends the DPMM class. Similarly to the GaussianDPMM class , it contains all the methods that are required to estimate the probabilities under the Multinomial-Dirichlet assumption and contains the static nested class Cluster which implements the abstract methods of DPMM.Cluster.
The SRS class is used to perform Simple Random Sampling from a frequency table. It is used by the Gibbs Sampler to estimate the new cluster assignments in each step of the iterative process.
The Point class serves as a tuple which stores the data of the record along with its id.
The Apache Commons Math 3.3 lib is used for Matrix multiplications and it is the only dependency of our implementation.
This class contains examples of how to use the Java implementation.
The user of the code is able to configure all the parameters of the mixture models, including the model types and the hyperparameters. In the following code snippet we can see how the algorithm is initialized and executed:
List<Point> pointList = new ArrayList<>();
//add records in pointList
//Dirichlet Process parameter
Integer dimensionality = 2;
double alpha = 1.0;
//Hyper parameters of Base Function
int kappa0 = 0;
int nu0 = 1;
RealVector mu0 = new ArrayRealVector(new double[]{0.0, 0.0});
RealMatrix psi0 = new BlockRealMatrix(new double[][]{{1.0,0.0},{0.0,1.0}});
//Create a DPMM object
DPMM dpmm = new GaussianDPMM(dimensionality, alpha, kappa0, nu0, mu0, psi0);
int maxIterations = 100;
int performedIterations = dpmm.cluster(pointList, maxIterations);
//get a list with the point ids and their assignments
Map<Integer, Integer> zi = dpmm.getPointAssignments();
Below we can see the results of running the algorithm on a synthetic dataset which consists of 300 data points. The points were generated originally by 3 different distributions: N([10,50], I), N([50,10], I) and N([150,100], I).
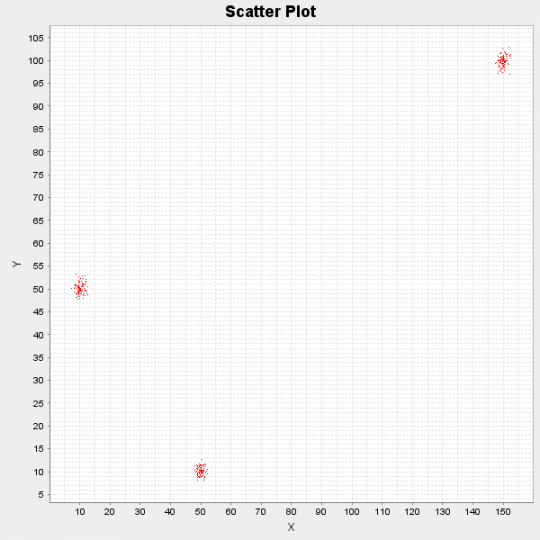
Figure 1: Scatter Plot of demo dataset
The algorithm after running for 10 iterations, it identified the following 3 cluster centres: [10.17, 50.11], [49.99, 10.13] and [149.97, 99.81]. Finally since we treat everything in a Bayesian manner, we are able not only to provide single point estimations of the cluster centres but also their probability distribution by using the formula 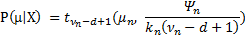 .
.
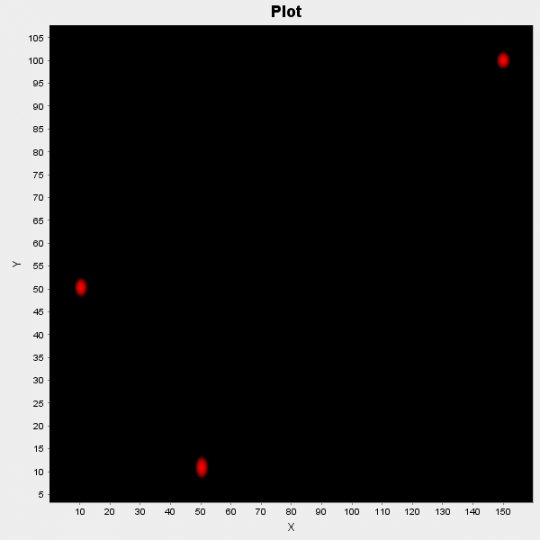
Figure 2: Scatter Plot of probabilities of clusters’ centers
In the figure above we plot those probabilities; the red areas indicate high probability of being center of a cluster and black areas indicate low probability.
To use the Java implementation in real world applications you must write external code that converts your original dataset into the required format. Moreover additional code might be necessary if you want to visualize the output as we see above. Finally note that the Apache Commons Math library is included in the project and thus no additional configuration is required to run the demos.
If you use the implementation in an interesting project drop us a line and we will feature your project on our blog. Also if you like the article, please take a moment and share it on Twitter or Facebook.
2013-2026 © Datumbox. All Rights Reserved. Privacy Policy | Terms of Use
I have a dataset generated from a particular Bayesian Network (BN) with random CPT values. Observation values for each random variable contains either 0 or 1. My goal is to obtain the same BN from generated data by using structure learning algorithms. If the BN has too many random variables, structure learning algorithms are not feasible due to computational cost. Therefore, I need to find modules in the data and apply structure learning for each modules. I was thinking to perform clustering to find modules, and since the data is generated under some distributions, DPMM would be a great choice.
Do you have any suggestions to cluster binary valued data? What classes should I define for this task?
Thanks for the great post series.