
UPDATE: Unfortunately my Pull-Request to Keras that changed the behaviour of the Batch Normalization layer was not accepted. You can read the details here. For those of you who are brave enough to mess with custom implementations, you can find the code in my branch. I might maintain it and merge it with the latest stable version of Keras (2.1.6, 2.2.2 and 2.2.4) for as long as I use it but no promises.
Most people who work in Deep Learning have either used or heard of Keras. For those of you who haven’t, it’s a great library that abstracts the underlying Deep Learning frameworks such as TensorFlow, Theano and CNTK and provides a high-level API for training ANNs. It is easy to use, enables fast prototyping and has a friendly active community. I’ve been using it heavily and contributing to the project periodically for quite some time and I definitely recommend it to anyone who wants to work on Deep Learning.
Even though Keras made my life easier, quite many times I’ve been bitten by the odd behavior of the Batch Normalization layer. Its default behavior has changed over time, nevertheless it still causes problems to many users and as a result there are several related open issues on Github. In this blog post, I will try to build a case for why Keras’ BatchNormalization layer does not play nice with Transfer Learning, I’ll provide the code that fixes the problem and I will give examples with the results of the patch.
On the subsections below, I provide an introduction on how Transfer Learning is used in Deep Learning, what is the Batch Normalization layer, how learnining_phase works and how Keras changed the BN behavior over time. If you already know these, you can safely jump directly to section 2.
One of the reasons why Deep Learning was criticized in the past is that it requires too much data. This is not always true; there are several techniques to address this limitation, one of which is Transfer Learning.
Assume that you are working on a Computer Vision application and you want to build a classifier that distinguishes Cats from Dogs. You don’t actually need millions of cat/dog images to train the model. Instead you can use a pre-trained classifier and fine-tune the top convolutions with less data. The idea behind it is that since the pre-trained model was fit on images, the bottom convolutions can recognize features like lines, edges and other useful patterns meaning you can use its weights either as good initialization values or partially retrain the network with your data.
Keras comes with several pre-trained models and easy-to-use examples on how to fine-tune models. You can read more on the documentation.
The Batch Normalization layer was introduced in 2014 by Ioffe and Szegedy. It addresses the vanishing gradient problem by standardizing the output of the previous layer, it speeds up the training by reducing the number of required iterations and it enables the training of deeper neural networks. Explaining exactly how it works is beyond the scope of this post but I strongly encourage you to read the original paper. An oversimplified explanation is that it rescales the input by subtracting its mean and by dividing with its standard deviation; it can also learn to undo the transformation if necessary.
Some layers operate differently during training and inference mode. The most notable examples are the Batch Normalization and the Dropout layers. In the case of BN, during training we use the mean and variance of the mini-batch to rescale the input. On the other hand, during inference we use the moving average and variance that was estimated during training.
Keras knows in which mode to run because it has a built-in mechanism called learning_phase. The learning phase controls whether the network is on train or test mode. If it is not manually set by the user, during fit() the network runs with learning_phase=1 (train mode). While producing predictions (for example when we call the predict() & evaluate() methods or at the validation step of the fit()) the network runs with learning_phase=0 (test mode). Even though it is not recommended, the user is also able to statically change the learning_phase to a specific value but this needs to happen before any model or tensor is added in the graph. If the learning_phase is set statically, Keras will be locked to whichever mode the user selected.
Keras has changed the behavior of Batch Normalization several times but the most recent significant update happened in Keras 2.1.3. Before v2.1.3 when the BN layer was frozen (trainable = False) it kept updating its batch statistics, something that caused epic headaches to its users.
This was not just a weird policy, it was actually wrong. Imagine that a BN layer exists between convolutions; if the layer is frozen no changes should happen to it. If we do update partially its weights and the next layers are also frozen, they will never get the chance to adjust to the updates of the mini-batch statistics leading to higher error. Thankfully starting from version 2.1.3, when a BN layer is frozen it no longer updates its statistics. But is that enough? Not if you are using Transfer Learning.
Below I describe exactly what is the problem and I sketch out the technical implementation for solving it. I also provide a few examples to show the effects on model’s accuracy before and after the patch is applied.
The problem with the current implementation of Keras is that when a BN layer is frozen, it continues to use the mini-batch statistics during training. I believe a better approach when the BN is frozen is to use the moving mean and variance that it learned during training. Why? For the same reasons why the mini-batch statistics should not be updated when the layer is frozen: it can lead to poor results because the next layers are not trained properly.
Assume you are building a Computer Vision model but you don’t have enough data, so you decide to use one of the pre-trained CNNs of Keras and fine-tune it. Unfortunately, by doing so you get no guarantees that the mean and variance of your new dataset inside the BN layers will be similar to the ones of the original dataset. Remember that at the moment, during training your network will always use the mini-batch statistics either the BN layer is frozen or not; also during inference you will use the previously learned statistics of the frozen BN layers. As a result, if you fine-tune the top layers, their weights will be adjusted to the mean/variance of the new dataset. Nevertheless, during inference they will receive data which are scaled differently because the mean/variance of the original dataset will be used.
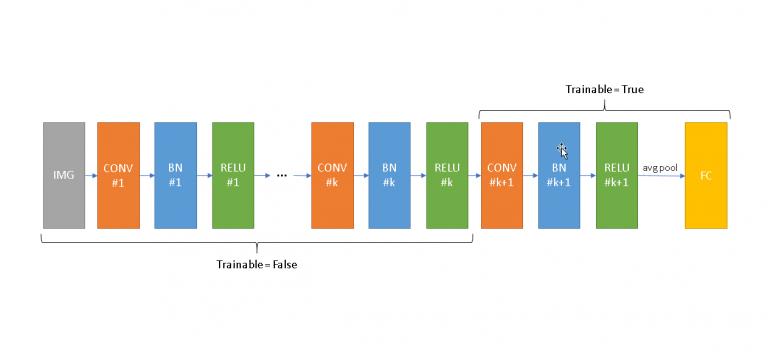
Above I provide a simplistic (and unrealistic) architecture for demonstration purposes. Let’s assume that we fine-tune the model from Convolution k+1 up until the top of the network (right side) and we keep frozen the bottom (left side). During training all BN layers from 1 to k will use the mean/variance of your training data. This will have negative effects on the frozen ReLUs if the mean and variance on each BN are not close to the ones learned during pre-training. It will also cause the rest of the network (from CONV k+1 and later) to be trained with inputs that have different scales comparing to what will receive during inference. During training your network can adapt to these changes, nevertheless the moment you switch to prediction-mode, Keras will use different standardization statistics, something that will swift the distribution of the inputs of the next layers leading to poor results.
One way to detect it is to set statically the learning phase of Keras to 1 (train mode) and to 0 (test mode) and evaluate your model in each case. If there is significant difference in accuracy on the same dataset, you are being affected by the problem. It’s worth pointing out that, due to the way the learning_phase mechanism is implemented in Keras, it is typically not advised to mess with it. Changes on the learning_phase will have no effect on models that are already compiled and used; as you can see on the examples on the next subsections, the best way to do this is to start with a clean session and change the learning_phase before any tensor is defined in the graph.
Another way to detect the problem while working with binary classifiers is to check the accuracy and the AUC. If the accuracy is close to 50% but the AUC is close to 1 (and also you observe differences between train/test mode on the same dataset), it could be that the probabilities are out-of-scale due the BN statistics. Similarly, for regression you can use MSE and Spearman’s correlation to detect it.
I believe that the problem can be fixed if the frozen BN layers are actually just that: permanently locked in test mode. Implementation-wise, the trainable flag needs to be part of the computational graph and the behavior of the BN needs to depend not only on the learning_phase but also on the value of the trainable property. You can find the details of my implementation on Github.
By applying the above fix, when a BN layer is frozen it will no longer use the mini-batch statistics but instead use the ones learned during training. As a result, there will be no discrepancy between training and test modes which leads to increased accuracy. Obviously when the BN layer is not frozen, it will continue using the mini-batch statistics during training.
Even though I wrote the above implementation recently, the idea behind it is heavily tested on real-world problems using various workarounds that have the same effect. For example, the discrepancy between training and testing modes and can be avoided by splitting the network in two parts (frozen and unfrozen) and performing cached training (passing data through the frozen model once and then using them to train the unfrozen network). Nevertheless, because the “trust me I’ve done this before” typically bears no weight, below I provide a few examples that show the effects of the new implementation in practice.
Here are a few important points about the experiment:
The code for the experiment is shown below:
import numpy as np
from keras.datasets import cifar10
from scipy.misc import imresize
from keras.preprocessing.image import ImageDataGenerator
from keras.applications.resnet50 import ResNet50, preprocess_input
from keras.models import Model, load_model
from keras.layers import Dense, Flatten
from keras import backend as K
seed = 42
epochs = 10
records_per_class = 100
# We take only 2 classes from CIFAR10 and a very small sample to intentionally overfit the model.
# We will also use the same data for train/test and expect that Keras will give the same accuracy.
(x, y), _ = cifar10.load_data()
def filter_resize(category):
# We do the preprocessing here instead in the Generator to get around a bug on Keras 2.1.5.
return [preprocess_input(imresize(img, (224,224)).astype('float')) for img in x[y.flatten()==category][:records_per_class]]
x = np.stack(filter_resize(3)+filter_resize(5))
records_per_class = x.shape[0] // 2
y = np.array([[1,0]]*records_per_class + [[0,1]]*records_per_class)
# We will use a pre-trained model and finetune the top layers.
np.random.seed(seed)
base_model = ResNet50(weights='imagenet', include_top=False, input_shape=(224, 224, 3))
l = Flatten()(base_model.output)
predictions = Dense(2, activation='softmax')(l)
model = Model(inputs=base_model.input, outputs=predictions)
for layer in model.layers[:140]:
layer.trainable = False
for layer in model.layers[140:]:
layer.trainable = True
model.compile(optimizer='sgd', loss='categorical_crossentropy', metrics=['accuracy'])
model.fit_generator(ImageDataGenerator().flow(x, y, seed=42), epochs=epochs, validation_data=ImageDataGenerator().flow(x, y, seed=42))
# Store the model on disk
model.save('tmp.h5')
# In every test we will clear the session and reload the model to force Learning_Phase values to change.
print('DYNAMIC LEARNING_PHASE')
K.clear_session()
model = load_model('tmp.h5')
# This accuracy should match exactly the one of the validation set on the last iteration.
print(model.evaluate_generator(ImageDataGenerator().flow(x, y, seed=42)))
print('STATIC LEARNING_PHASE = 0')
K.clear_session()
K.set_learning_phase(0)
model = load_model('tmp.h5')
# Again the accuracy should match the above.
print(model.evaluate_generator(ImageDataGenerator().flow(x, y, seed=42)))
print('STATIC LEARNING_PHASE = 1')
K.clear_session()
K.set_learning_phase(1)
model = load_model('tmp.h5')
# The accuracy will be close to the one of the training set on the last iteration.
print(model.evaluate_generator(ImageDataGenerator().flow(x, y, seed=42)))
Let’s check the results on Keras v2.1.5:
Epoch 1/10 1/7 [===>..........................] - ETA: 25s - loss: 0.8751 - acc: 0.5312 2/7 [=======>......................] - ETA: 11s - loss: 0.8594 - acc: 0.4531 3/7 [===========>..................] - ETA: 7s - loss: 0.8398 - acc: 0.4688 4/7 [================>.............] - ETA: 4s - loss: 0.8467 - acc: 0.4844 5/7 [====================>.........] - ETA: 2s - loss: 0.7904 - acc: 0.5437 6/7 [========================>.....] - ETA: 1s - loss: 0.7593 - acc: 0.5625 7/7 [==============================] - 12s 2s/step - loss: 0.7536 - acc: 0.5744 - val_loss: 0.6526 - val_acc: 0.6650 Epoch 2/10 1/7 [===>..........................] - ETA: 4s - loss: 0.3881 - acc: 0.8125 2/7 [=======>......................] - ETA: 3s - loss: 0.3945 - acc: 0.7812 3/7 [===========>..................] - ETA: 2s - loss: 0.3956 - acc: 0.8229 4/7 [================>.............] - ETA: 1s - loss: 0.4223 - acc: 0.8047 5/7 [====================>.........] - ETA: 1s - loss: 0.4483 - acc: 0.7812 6/7 [========================>.....] - ETA: 0s - loss: 0.4325 - acc: 0.7917 7/7 [==============================] - 8s 1s/step - loss: 0.4095 - acc: 0.8089 - val_loss: 0.4722 - val_acc: 0.7700 Epoch 3/10 1/7 [===>..........................] - ETA: 4s - loss: 0.2246 - acc: 0.9375 2/7 [=======>......................] - ETA: 3s - loss: 0.2167 - acc: 0.9375 3/7 [===========>..................] - ETA: 2s - loss: 0.2260 - acc: 0.9479 4/7 [================>.............] - ETA: 2s - loss: 0.2179 - acc: 0.9375 5/7 [====================>.........] - ETA: 1s - loss: 0.2356 - acc: 0.9313 6/7 [========================>.....] - ETA: 0s - loss: 0.2392 - acc: 0.9427 7/7 [==============================] - 8s 1s/step - loss: 0.2288 - acc: 0.9456 - val_loss: 0.4282 - val_acc: 0.7800 Epoch 4/10 1/7 [===>..........................] - ETA: 4s - loss: 0.2183 - acc: 0.9688 2/7 [=======>......................] - ETA: 3s - loss: 0.1899 - acc: 0.9844 3/7 [===========>..................] - ETA: 2s - loss: 0.1887 - acc: 0.9792 4/7 [================>.............] - ETA: 1s - loss: 0.1995 - acc: 0.9531 5/7 [====================>.........] - ETA: 1s - loss: 0.1932 - acc: 0.9625 6/7 [========================>.....] - ETA: 0s - loss: 0.1819 - acc: 0.9688 7/7 [==============================] - 8s 1s/step - loss: 0.1743 - acc: 0.9747 - val_loss: 0.3778 - val_acc: 0.8400 Epoch 5/10 1/7 [===>..........................] - ETA: 3s - loss: 0.0973 - acc: 1.0000 2/7 [=======>......................] - ETA: 3s - loss: 0.0828 - acc: 1.0000 3/7 [===========>..................] - ETA: 2s - loss: 0.0851 - acc: 1.0000 4/7 [================>.............] - ETA: 1s - loss: 0.0897 - acc: 1.0000 5/7 [====================>.........] - ETA: 1s - loss: 0.0928 - acc: 1.0000 6/7 [========================>.....] - ETA: 0s - loss: 0.0936 - acc: 1.0000 7/7 [==============================] - 8s 1s/step - loss: 0.1337 - acc: 0.9838 - val_loss: 0.3916 - val_acc: 0.8100 Epoch 6/10 1/7 [===>..........................] - ETA: 4s - loss: 0.0747 - acc: 1.0000 2/7 [=======>......................] - ETA: 3s - loss: 0.0852 - acc: 1.0000 3/7 [===========>..................] - ETA: 2s - loss: 0.0812 - acc: 1.0000 4/7 [================>.............] - ETA: 1s - loss: 0.0831 - acc: 1.0000 5/7 [====================>.........] - ETA: 1s - loss: 0.0779 - acc: 1.0000 6/7 [========================>.....] - ETA: 0s - loss: 0.0766 - acc: 1.0000 7/7 [==============================] - 8s 1s/step - loss: 0.0813 - acc: 1.0000 - val_loss: 0.3637 - val_acc: 0.8550 Epoch 7/10 1/7 [===>..........................] - ETA: 1s - loss: 0.2478 - acc: 0.8750 2/7 [=======>......................] - ETA: 2s - loss: 0.1966 - acc: 0.9375 3/7 [===========>..................] - ETA: 2s - loss: 0.1528 - acc: 0.9583 4/7 [================>.............] - ETA: 1s - loss: 0.1300 - acc: 0.9688 5/7 [====================>.........] - ETA: 1s - loss: 0.1193 - acc: 0.9750 6/7 [========================>.....] - ETA: 0s - loss: 0.1196 - acc: 0.9792 7/7 [==============================] - 8s 1s/step - loss: 0.1084 - acc: 0.9838 - val_loss: 0.3546 - val_acc: 0.8600 Epoch 8/10 1/7 [===>..........................] - ETA: 4s - loss: 0.0539 - acc: 1.0000 2/7 [=======>......................] - ETA: 2s - loss: 0.0900 - acc: 1.0000 3/7 [===========>..................] - ETA: 2s - loss: 0.0815 - acc: 1.0000 4/7 [================>.............] - ETA: 1s - loss: 0.0740 - acc: 1.0000 5/7 [====================>.........] - ETA: 1s - loss: 0.0700 - acc: 1.0000 6/7 [========================>.....] - ETA: 0s - loss: 0.0701 - acc: 1.0000 7/7 [==============================] - 8s 1s/step - loss: 0.0695 - acc: 1.0000 - val_loss: 0.3269 - val_acc: 0.8600 Epoch 9/10 1/7 [===>..........................] - ETA: 4s - loss: 0.0306 - acc: 1.0000 2/7 [=======>......................] - ETA: 3s - loss: 0.0377 - acc: 1.0000 3/7 [===========>..................] - ETA: 2s - loss: 0.0898 - acc: 0.9583 4/7 [================>.............] - ETA: 1s - loss: 0.0773 - acc: 0.9688 5/7 [====================>.........] - ETA: 1s - loss: 0.0742 - acc: 0.9750 6/7 [========================>.....] - ETA: 0s - loss: 0.0708 - acc: 0.9792 7/7 [==============================] - 8s 1s/step - loss: 0.0659 - acc: 0.9838 - val_loss: 0.3604 - val_acc: 0.8600 Epoch 10/10 1/7 [===>..........................] - ETA: 3s - loss: 0.0354 - acc: 1.0000 2/7 [=======>......................] - ETA: 3s - loss: 0.0381 - acc: 1.0000 3/7 [===========>..................] - ETA: 2s - loss: 0.0354 - acc: 1.0000 4/7 [================>.............] - ETA: 1s - loss: 0.0828 - acc: 0.9688 5/7 [====================>.........] - ETA: 1s - loss: 0.0791 - acc: 0.9750 6/7 [========================>.....] - ETA: 0s - loss: 0.0794 - acc: 0.9792 7/7 [==============================] - 8s 1s/step - loss: 0.0704 - acc: 0.9838 - val_loss: 0.3615 - val_acc: 0.8600 DYNAMIC LEARNING_PHASE [0.3614931714534759, 0.86] STATIC LEARNING_PHASE = 0 [0.3614931714534759, 0.86] STATIC LEARNING_PHASE = 1 [0.025861846953630446, 1.0]
As we can see above, during training the model learns very well the data and achieves on the training set near-perfect accuracy. Still at the end of each iteration, while evaluating the model on the same dataset, we get significant differences in loss and accuracy. Note that we should not be getting this; we have overfitted intentionally the model on the specific dataset and the training/validation datasets are identical.
After the training is completed we evaluate the model using 3 different learning_phase configurations: Dynamic, Static = 0 (test mode) and Static = 1 (training mode). As we can see the first two configurations will provide identical results in terms of loss and accuracy and their value matches the reported accuracy of the model on the validation set in the last iteration. Nevertheless, once we switch to training mode, we observe a massive discrepancy (improvement). Why it that? As we said earlier, the weights of the network are tuned expecting to receive data scaled with the mean/variance of the training data. Unfortunately, those statistics are different from the ones stored in the BN layers. Since the BN layers were frozen, these statistics were never updated. This discrepancy between the values of the BN statistics leads to the deterioration of the accuracy during inference.
Let’s see what happens once we apply the patch:
Epoch 1/10 1/7 [===>..........................] - ETA: 26s - loss: 0.9992 - acc: 0.4375 2/7 [=======>......................] - ETA: 12s - loss: 1.0534 - acc: 0.4375 3/7 [===========>..................] - ETA: 7s - loss: 1.0592 - acc: 0.4479 4/7 [================>.............] - ETA: 4s - loss: 0.9618 - acc: 0.5000 5/7 [====================>.........] - ETA: 2s - loss: 0.8933 - acc: 0.5250 6/7 [========================>.....] - ETA: 1s - loss: 0.8638 - acc: 0.5417 7/7 [==============================] - 13s 2s/step - loss: 0.8357 - acc: 0.5570 - val_loss: 0.2414 - val_acc: 0.9450 Epoch 2/10 1/7 [===>..........................] - ETA: 4s - loss: 0.2331 - acc: 0.9688 2/7 [=======>......................] - ETA: 2s - loss: 0.3308 - acc: 0.8594 3/7 [===========>..................] - ETA: 2s - loss: 0.3986 - acc: 0.8125 4/7 [================>.............] - ETA: 1s - loss: 0.3721 - acc: 0.8281 5/7 [====================>.........] - ETA: 1s - loss: 0.3449 - acc: 0.8438 6/7 [========================>.....] - ETA: 0s - loss: 0.3168 - acc: 0.8646 7/7 [==============================] - 9s 1s/step - loss: 0.3165 - acc: 0.8633 - val_loss: 0.1167 - val_acc: 0.9950 Epoch 3/10 1/7 [===>..........................] - ETA: 1s - loss: 0.2457 - acc: 1.0000 2/7 [=======>......................] - ETA: 2s - loss: 0.2592 - acc: 0.9688 3/7 [===========>..................] - ETA: 2s - loss: 0.2173 - acc: 0.9688 4/7 [================>.............] - ETA: 1s - loss: 0.2122 - acc: 0.9688 5/7 [====================>.........] - ETA: 1s - loss: 0.2003 - acc: 0.9688 6/7 [========================>.....] - ETA: 0s - loss: 0.1896 - acc: 0.9740 7/7 [==============================] - 9s 1s/step - loss: 0.1835 - acc: 0.9773 - val_loss: 0.0678 - val_acc: 1.0000 Epoch 4/10 1/7 [===>..........................] - ETA: 1s - loss: 0.2051 - acc: 1.0000 2/7 [=======>......................] - ETA: 2s - loss: 0.1652 - acc: 0.9844 3/7 [===========>..................] - ETA: 2s - loss: 0.1423 - acc: 0.9896 4/7 [================>.............] - ETA: 1s - loss: 0.1289 - acc: 0.9922 5/7 [====================>.........] - ETA: 1s - loss: 0.1225 - acc: 0.9938 6/7 [========================>.....] - ETA: 0s - loss: 0.1149 - acc: 0.9948 7/7 [==============================] - 9s 1s/step - loss: 0.1060 - acc: 0.9955 - val_loss: 0.0455 - val_acc: 1.0000 Epoch 5/10 1/7 [===>..........................] - ETA: 4s - loss: 0.0769 - acc: 1.0000 2/7 [=======>......................] - ETA: 2s - loss: 0.0846 - acc: 1.0000 3/7 [===========>..................] - ETA: 2s - loss: 0.0797 - acc: 1.0000 4/7 [================>.............] - ETA: 1s - loss: 0.0736 - acc: 1.0000 5/7 [====================>.........] - ETA: 1s - loss: 0.0914 - acc: 1.0000 6/7 [========================>.....] - ETA: 0s - loss: 0.0858 - acc: 1.0000 7/7 [==============================] - 9s 1s/step - loss: 0.0808 - acc: 1.0000 - val_loss: 0.0346 - val_acc: 1.0000 Epoch 6/10 1/7 [===>..........................] - ETA: 1s - loss: 0.1267 - acc: 1.0000 2/7 [=======>......................] - ETA: 2s - loss: 0.1039 - acc: 1.0000 3/7 [===========>..................] - ETA: 2s - loss: 0.0893 - acc: 1.0000 4/7 [================>.............] - ETA: 1s - loss: 0.0780 - acc: 1.0000 5/7 [====================>.........] - ETA: 1s - loss: 0.0758 - acc: 1.0000 6/7 [========================>.....] - ETA: 0s - loss: 0.0789 - acc: 1.0000 7/7 [==============================] - 9s 1s/step - loss: 0.0738 - acc: 1.0000 - val_loss: 0.0248 - val_acc: 1.0000 Epoch 7/10 1/7 [===>..........................] - ETA: 4s - loss: 0.0344 - acc: 1.0000 2/7 [=======>......................] - ETA: 3s - loss: 0.0385 - acc: 1.0000 3/7 [===========>..................] - ETA: 3s - loss: 0.0467 - acc: 1.0000 4/7 [================>.............] - ETA: 1s - loss: 0.0445 - acc: 1.0000 5/7 [====================>.........] - ETA: 1s - loss: 0.0446 - acc: 1.0000 6/7 [========================>.....] - ETA: 0s - loss: 0.0429 - acc: 1.0000 7/7 [==============================] - 9s 1s/step - loss: 0.0421 - acc: 1.0000 - val_loss: 0.0202 - val_acc: 1.0000 Epoch 8/10 1/7 [===>..........................] - ETA: 4s - loss: 0.0319 - acc: 1.0000 2/7 [=======>......................] - ETA: 3s - loss: 0.0300 - acc: 1.0000 3/7 [===========>..................] - ETA: 3s - loss: 0.0320 - acc: 1.0000 4/7 [================>.............] - ETA: 2s - loss: 0.0307 - acc: 1.0000 5/7 [====================>.........] - ETA: 1s - loss: 0.0303 - acc: 1.0000 6/7 [========================>.....] - ETA: 0s - loss: 0.0291 - acc: 1.0000 7/7 [==============================] - 9s 1s/step - loss: 0.0358 - acc: 1.0000 - val_loss: 0.0167 - val_acc: 1.0000 Epoch 9/10 1/7 [===>..........................] - ETA: 4s - loss: 0.0246 - acc: 1.0000 2/7 [=======>......................] - ETA: 3s - loss: 0.0255 - acc: 1.0000 3/7 [===========>..................] - ETA: 3s - loss: 0.0258 - acc: 1.0000 4/7 [================>.............] - ETA: 2s - loss: 0.0250 - acc: 1.0000 5/7 [====================>.........] - ETA: 1s - loss: 0.0252 - acc: 1.0000 6/7 [========================>.....] - ETA: 0s - loss: 0.0260 - acc: 1.0000 7/7 [==============================] - 9s 1s/step - loss: 0.0327 - acc: 1.0000 - val_loss: 0.0143 - val_acc: 1.0000 Epoch 10/10 1/7 [===>..........................] - ETA: 4s - loss: 0.0251 - acc: 1.0000 2/7 [=======>......................] - ETA: 2s - loss: 0.0228 - acc: 1.0000 3/7 [===========>..................] - ETA: 2s - loss: 0.0217 - acc: 1.0000 4/7 [================>.............] - ETA: 1s - loss: 0.0249 - acc: 1.0000 5/7 [====================>.........] - ETA: 1s - loss: 0.0244 - acc: 1.0000 6/7 [========================>.....] - ETA: 0s - loss: 0.0239 - acc: 1.0000 7/7 [==============================] - 9s 1s/step - loss: 0.0290 - acc: 1.0000 - val_loss: 0.0127 - val_acc: 1.0000 DYNAMIC LEARNING_PHASE [0.012697912137955427, 1.0] STATIC LEARNING_PHASE = 0 [0.012697912137955427, 1.0] STATIC LEARNING_PHASE = 1 [0.01744014158844948, 1.0]
First of all, we observe that the network converges significantly faster and achieves perfect accuracy. We also see that there is no longer a discrepancy in terms of accuracy when we switch between different learning_phase values.
So how does the patch perform on a more realistic experiment? Let’s use Keras’ pre-trained ResNet50 (originally fit on imagenet), remove the top classification layer and fine-tune it with and without the patch and compare the results. For data, we will use CIFAR10 (the standard train/test split provided by Keras) and we will resize the images to 224×224 to make them compatible with the ResNet50’s input size.
We will do 10 epochs to train the top classification layer using RSMprop and then we will do another 5 to fine-tune everything after the 139th layer using SGD(lr=1e-4, momentum=0.9). Without the patch our model achieves an accuracy of 87.44%. Using the patch, we get an accuracy of 92.36%, almost 5 points higher.
Batch Normalization is not the only layer that operates differently between train and test modes. Dropout and its variants also have the same effect. Should we apply the same policy to all these layers? I believe not (even though I would love to hear your thoughts on this). The reason is that Dropout is used to avoid overfitting, thus locking it permanently to prediction mode during training would defeat its purpose. What do you think?
I strongly believe that this discrepancy must be solved in Keras. I’ve seen even more profound effects (from 100% down to 50% accuracy) in real-world applications caused by this problem. I plan to send already sent a PR to Keras with the fix and hopefully it will be accepted.
If you liked this blogpost, please take a moment to share it on Facebook or Twitter. 🙂
2013-2024 © Datumbox. All Rights Reserved. Privacy Policy | Terms of Use
So based on the dropout case, would you argue that it shouldn’t just be the case that learning_phase is set to zero for all “frozen” layers (and anything that depends on them, ignoring the complications at the borders)? I think, re: dropout, it’s unclear to me that using it w/in the frozen layers provides useful regularization — I suppose this is easy enough to test empirically however.
But basically, my view is that if you’re going to freeze some lower parts of the representation chain, I feel like it should be equivalent to running that model in prediction mode up to that layer of representation, and just handing the resulting features off to the next model as if it’s a wholly separate (i.e., non-differentiable) discontinuity (e.g. in Sharif Razavian, A., Azizpour, H., Sullivan, J., & Carlsson, S. (2014). CNN Features off-the-shelf: an Astounding Baseline for Recognition. arXiv Preprint arXiv:1403.6382. Retrieved from https://adsabs.harvard.edu/abs/2014arXiv1403.6382S). To keep dropout going before you reach the training model is weird, although I’m not confident that it’s necessarily worse.
Additionally, how would you apply this in the case where you’re not freezing the transferred layers, but dramatically decreasing their learning rate (e.g. discriminative fine-tuning from Howard, J., & Ruder, S. (2018). Fine-tuned Language Models for Text Classification. Retrieved from https://arxiv.org/abs/1801.06146)? I think it’d make sense to continue updating the mini-batch statistics here since they’ll be changing proportional to the new learning rate regardless, but would love to hear your thoughts.
Hi Zach,
Thanks for the comment.
I personally would not change the behaviour of the Dropout. Having said that, I agree with your remark that freezing the network should be equivalent to splitting the network into two parts, using half of it for prediction and train only the latter. This is a standard workaround I’ve been doing before deciding to properly patch this and submit a PR.
I also agree that as long as you are updating the model you should update the mini-batch statistics, even if you are decreasing dramatically the learning rate. In this specific case, you should probably also change the momentum of the BN layer to avoid updating the mini-batch statistics so aggressively. Of course this is not straightforward because momentum is not part of the computational graph and thus changing the value after the definition will have no effect. A “nasty but easy” solution is to serialize the model, modify programmatically the JSON schema and load it back (sucks but works).
Vasilis,
In the example, all of the layers up to 140 had the trainable flag set to False. What would happen if you had taken the time to set this flag to True for just the batch normalization layers?
In my experience with transfer learning it’s good to train the whole network on the new data set, and then freeze the feature layers to train just the classification layers to get a bit more improvement.
Hello Wade,
Thanks for your comment.
First of all to address your second remark, I agree. When you have enough data to fine-tune the whole network this is what you should do. You will have a greating starting point for the weights (provided that not many neurons are dead due to relus) and you will get good accuracy. Unfortunately, there are cases where you don’t have enough data for training the model end-to-end. Imagine if you use a classifier trained on the same domain but now you want to reuse it on a different problem where you have significantly less annotated data. In such a case, your best bet is to fine-tune part of the network to avoid overfitting. This is where the current Keras behaviour can bite you.
Concerning unfreezing the BNs before 140, this is something that will not work. Indeed the BN will update its mean/var (and it will match the ones of your training data) but the frozen convolutions and non-linearities after the BNs will not be updated to “see” this difference on the scaling. This will cause again discrepancies and lower accuracy. As it is your safest bet is to split the network into two parts: the frozen model will operate in Inference mode and provide you with data and the trainable model that gets trained with the output of the frozen. Those two can’t be connected on the graph, so this is a messy and hacky solution.
Thanks for the blogpost. After some investigation I noticed the exact same problem last week and was looking for a solution to force inference mode for batchnorm layers. I ended up splitting the model into two parts, which is very impractical and hacky, especially when I’m using online data augmentation. I see no reason why batch statistics should be used instead of precomputed ones when the layer is frozen, too bad fchollet has a different opinion.
Thank you very much for your diligence! I have had similar problems with fine tuning in Keras/TF which I thought were related to skip connections in Keras but now I see their root cause is the batchnorm implementation as it is written. This has significant implications for those trying to train more advanced models in Keras/TF with fine tuning. Hopefully it will be addressed.
Thank you Vasilis. You saved the day. I went into a ResNet50 fine tuning train start with accuracy = 0.0~0.3 with its own predicted data as train and test datasets (10 classes). Even with all layer trainable = False, it showed ~0.3 train accuracy while val_acc=1.0 while training in every epoch. Gonna try to set phase to see if it was this BN layer caused problem here. But I believe it is.
Thanks for the article.
I have encountered this problem a couple of days ago. Unfortunately I did not find your blog right away, so had to spend a day trying to figure out what’s wrong with my model. The solution I found is to set all BN layers to trainable, so that they can adjust to my custom dataset.
Here is the discussion on stackowerflow
https://stackoverflow.com/questions/51123198/strange-behaviour-of-the-loss-function-in-keras-model-with-pretrained-convoluti/51124511#51124511
It happened before I found your blog, put the link to it in the update.
Thank you very much for your contribution. I had problems using BatchNormalization in my GAN models, and I had to use a custom fix that only marginally solved the problem. With your implementation, I now have a perfectly working model that gives consistent loss values when using BN.
Thank you again for this!
Glad it helped you! 🙂
Great post, I came to Keras yesterday specifically for how easy it is to implement transfer learning — and deciding how to deal with BN for non-VGG models came to my attention very quickly. This helps to clear a lot of things up, thanks!
Thanks for your efforts in investigating fixing this issue. Are there any plans by the maintainer of keras to integrate this fix? Or is there a pull request that can be tracked?
There is a pull-request but the maintainer decided not to merge. You can read the rational in the thread. Because many people face similar problems, I maintain a fork of the latest versions of Keras. Check on the blogpost for updated links.
Hello Vasillis,
I am having similar problems as described in you post. I am fine-tuning MobileNet and ResNet50 , getting bad results while predicting on train set itself. With VGG16 predict on train set reproduces loss and metric as reported during training. So it indeed looks like BN issue. However, this happens even if I make all layers trainable.
Anyhow, for MobileNet and ResNet50, when setting LEARNING_PHASE = 1, predict on train set indeed reproduces loss and metric as reported during training.
I managed to reproduce the results you present here, testing on official keras 2.1.6 and on your 2.1.6 branch. Official keras fails, but only when the lower layers are not trainable, otherwise your version provide no advantage, as expected (BTW keras 2.2.2 fails in both cases, all trainable or not ). Though it doesn’t seem my case, I tested my code with your branch, but it didn’t help.
Can you think of what might be the cause to the problem I’m having: Difference in training and test mode which is related to batch normalization, but even if all the layers are trainable?
Thanks,
Yonatan
You are most likely overfitting the network. Unless you have A LOT of data, training the entire network end-to-end will cause the network to overfit, leading to poor generalization.
The problem I reported yesterday was solved by using fit_generator instead of fit. However, I don’t understand how. I first thought it might be due to the shuffle, but it works also when I turn shuffle off.
Thanks anyhow.
It does works better than the original version。 Nevertheless, I still meet some issues when using it in GAN models. You will easily find that it is slower than Dropout in the Keras example’s DCGAN, and it does not work for a semi-supervisor GAN model. I mean the Keras’ original BN doesn’t work at all for GAN model, and your version is better than it, however, still with some problems.
I think some of the slowdown can be explained by the introduction of extra nodes on the execution graph. You can try freezing the graph during inference using TensorRT. As for the dcgan, I can’t be certain what the problem that you describe is. It’s worth running the whole thing with a debugger and a TFboard to trace down your problem.
Thank you very much Vasilis for this important clarification.
While I still have a doubt here: During fine-tuning, if the BNs are permanently locked (not updated), as suggested in your proposal, AND if the distribution of the new dataset IS indeed different from the original one (i.e ImageNet), will this discrepancy affect the training anyway?
To put it simple, assume that the orignal dataset has distribution D1, while the new dataset has distribution D2, D2 != D1. During fine-tuning, the BNs has D1, while mini-batch has D2. Will that be problematic ?
Thank you again !
I guess I am missing something. The Keras 2.1.3 release notes (15 January 2018) specifically seems to address this problem: “trainable attribute in BatchNormalization now disables the updates of the batch statistics (i.e. if trainable == False the layer will now run 100% in inference mode).”
Ref: https://github.com/keras-team/keras/releases/tag/2.1.3
I can’t understand. You say Keras don’t update mini batch statistics since 2.1.3. in section 1.4. But you also say “During training all BN layers from 1 to k will use the mean/variance of your training data”, which I think it means that mini batch statistics still continues in current version.
I also have this problem. My problem is that I cant install the patch on the server I’m working on. Is there a hack to achieve the same results as from using this patch?
One more question:
Is this how to install your patch?
pip3.6 install -U –force-reinstall –no-dependencies git+https://github.com/datumbox/keras.git
I can’t just get a huge help and go on my way.
You have a deep understanding in how the Keras’s BN implementation works and explained so well with such details.
You definitely saved my day and my project. I still don’t understand why Keras doesn’t accept your fork. (afraid to read through all the debates though.)
Hi Vasilis,
thank you for your effort you put towards this issue (it’s shame that they didn’t merge your commit!). I am working with relatively small datasets (80-100 images) and I don’t have any other options how to train neural network except freezing most of the layers and fine-tune the others.
My model behaves very well (around 80% accuracy over VGG16 but I can’t get more than 50% on any other keras-included models (I can’t find any other model that doesn’t use the BN).
I am using tensorflow keras api ( so no “the” keras) and I don’t know how can I fix the issue. set_learning_phase(0) and set_learning_phase(1) doesn’t work as expected.
See the code:
base_model = Xception(include_top=False, weights=’imagenet’)
set_learning_phase(0)
for layer in base_model.layers:
layer.trainable = False
x = base_model.output
set_learning_phase(1)
x = GlobalAveragePooling2D()(x)
x = Dense(32, activation=’relu’)(x)
predictions = Dense(1, activation=’sigmoid’)(x)
self.model = Model(inputs=base_model.input, outputs=predictions)
Thanks!
Thanks for your effort, it throws light on the dilemma I’ve been faced with, I will try it out.
By the way, when I am using Keras’s Batch Normalization to train a new model (not fine-tuning) with my data, the training loss continues to decrease and training acc increases, but the validation loss shifts dramatically (sorry for my poor English) while validation acc seems to remain the same (quite similar to random, like 0.5 in 2-class classification). Do you know how to deal with this kind of problem? Thank you!
Hi Vasilis,
Thanks for the post and the time you spent coming up with a solution and explaining it. I read the thread here and the one you started on GitHub. A lot of people agree with your solution and claim it worked for them. Which makes me wonder why it was not merged.
Anyways, I am writing because I don’t get better results after installing your patch “pip install -U –force-reinstall –no-dependencies git+https://github.com/datumbox/keras@fork/keras2.2.4”
Although training and validation performance mirrors each other, it seems the model stops training after the 1st/2nd epoch. The training loss and accuracy remain static after the 2nd epoch. I ran this on tf 1.12.2 and 1.13.1 and still had the same issue.
Your thoughts?
Hi Vasilis,
Thanks for the great blog , I spent a full 10 hours just reading all possible github and stackoverflow posts on this issue, and yet I couldn’t know for sure if my problem is a result of Bachnormalization behavior. I appreciate if you can answer me based on what I have
1- I used Densnet121 which is pretrained on Imagenet, which has the BN layers.
2- I am using tf.keras instead of standalon keras.
3- I didn’t freeze any layer.
4- I used the model to train facial emotions dataset which has a train, validation, test sets.
5- I am working on a regression problem for valence and arousal using euclidean distance loss and rmse as an evaluation metric.
The problem is:
1- When I feed my (train, val) to model.fit and use test set in model.evaluate then I got 17 on the validation rmse that is calculated during model.fit and 24 on test rmse that is calculated on model.evalute. But If I feed ( train, test) to model.fit the result for test rmse is different than the previous one because it is now calculated through model.fit not through model.evalute. I got 13 on test set ( lower is better). Basically the result with model.fit is better than the one calculated through model.evalute.
You will do to me a huge favor if you can tell me what you think the problem is here? Is this related to the batch normalization layer behavior
Hello, is there a release date for this fix in TF ? 😀
TF2 actually changed the semantics of the BN to operate exactly as proposed on my PR, so this problem is resolved in TF2 keras.
Hello, do you think this issue is related to this? https://stackoverflow.com/questions/69649917/batchnorm-makes-accuracy-at-prediction-time-around-10-of-whats-reported-during