 EDIT: This article is obsolete as it’s written before the development of many modern Deep Learning techniques. I advise you to look for newer sources on this topic.
EDIT: This article is obsolete as it’s written before the development of many modern Deep Learning techniques. I advise you to look for newer sources on this topic.
In most Supervised Machine Learning problems we need to define a model and estimate its parameters based on a training dataset. A popular and easy-to-use technique to calculate those parameters is to minimize model’s error with Gradient Descent. The Gradient Descent estimates the weights of the model in many iterations by minimizing a cost function at every step.
Here is the algorithm:
Repeat until convergence {
Wj = Wj - λ θF(Wj)/θWj
}
Where Wj is one of our parameters (or a vector with our parameters), F is our cost function (estimates the errors of our model), θF(Wj)/θWj is its first derivative with respect to Wj and λ is the learning rate.
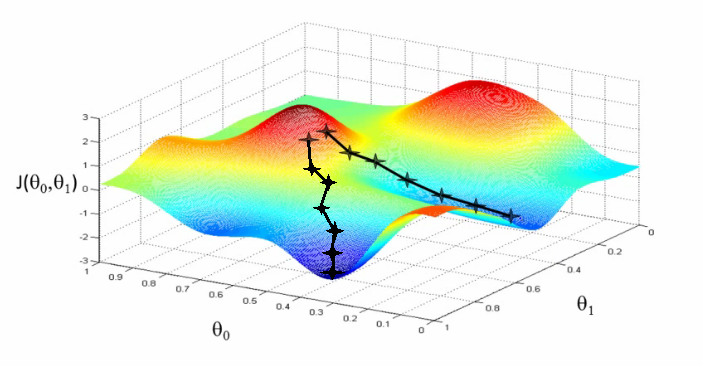
If our F is monotonic, this method will give us after many iterations an estimation of the Wj weights which minimize the cost function. Note that if the derivative is not monotonic we might be trapped to local minimum. In that case an easy way to detect this is by repeating the process for different initial Wj values and comparing the value of the cost function for the new estimated parameters.
Gradient Descent is not always the best method to calculate the weights, nevertheless it is a relatively fast and easy method. If you want to read more about Gradient Descent check out the notes of Ng for Stanford’s Machine Learning course.
In order for Gradient Descent to work we must set the λ (learning rate) to an appropriate value. This parameter determines how fast or slow we will move towards the optimal weights. If the λ is very large we will skip the optimal solution. If it is too small we will need too many iterations to converge to the best values. So using a good λ is crucial.
Depending on the cost function F that we will select, we might face different problems. When the Sum of Squared Errors is selected as our cost function then the value of θF(Wj)/θWj gets larger and larger as we increase the size of the training dataset. Thus the λ must be adapted to significantly smaller values.
One way to resolve this problem is to divide the λ with 1/N, where N is the size of the training data. So the update step of the algorithm can be rewritten as:
Wj = Wj - (λ/N)*θF(Wj)/θWj
You can read more about this on Wilson et al. paper “The general inefficiency of batch training for gradient descent learning”.
Finally another way to resolve this problem is by selecting a cost function that is not affected by the number of train examples that we use, such as the Mean Squared Errors.
Another good technique is to adapt the value of λ in each iteration. The idea behind this is that the farther you are from optimal values the faster you should move towards the solution and thus the value of λ should be larger. The closer you get to the solution the smaller its value should be. Unfortunately since you don’t know the actual optimal values, you also don’t know how close you are to them in each step.
To resolve this you can check the value of the error function by using the estimated parameters of the model at the end of each iteration. If your error rate was reduced since the last iteration, you can try increasing the learning rate by 5%. If your error rate was actually increased (meaning that you skipped the optimal point) you should reset the values of Wj to the values of the previous iteration and decrease the learning rate by 50%. This technique is called Bold Driver.
In many machine learning problems normalizing the input vectors is a pretty common practice. In some techniques normalization is required because they internally use distances or feature variances and thus without normalization the results would be heavily affected by the feature with the largest variance or scale. Normalizing your inputs can also help your numerical optimization method (such as Gradient Descent) converge much faster and accurately.
Even though there are several ways to normalize a variable, the [0,1] normalization (also known as min-max) and the z-score normalization are two of the most widely used. Here is how you can calculate both of them:
XminmaxNorm = (X - min(X))/(max(X)-min(X)); XzscoreNorm = (X - mean(X))/std(X);
Hope this works for you! 🙂
Did you like the article? Please take a minute to share it on Twitter. 🙂
2013-2024 © Datumbox. All Rights Reserved. Privacy Policy | Terms of Use
Hi Mark,
This article is about adapting the learning rate in problems where iterative methods are used. I don’t cover anything about virtualizing the geometry. Depending on the software that you use to train the ANN, you might have a visualization tool. For example Matlab allows you to see visually the model while you design it.
Hi Caio,
Check out this paper: https://arxiv.org/pdf/1206.1106.pdf
I’m sure you will find it interesting. 🙂
in logistic regression for classification cost function is convex or non-convex can anyone explain this? ty
In “Adapting learning rate in each iteration” part, in the second paragraph if the error rate is reduced ,then why should the learning rate be increased ? As according to the first paragraph when we reach near to the solution then the learning rate should be small. So on decreasing the error rate we are moving towards the solution so why to increase the learning rate?
Have a look on the Bold Driver algorithm here, the provide a very intuitive explanation. Keep in mind this is not a state of the art optimizer to be used in Deep Learning models. It’s more for simpler optimization trick for the pre-deep learning era.